三角 関数 の 合成 例題

南北 に 長い 土地 間取り 南 玄関三角関数の合成公式（証明・問題・cos型について） - 理系ラボ. 1. 三角関数の合成公式（sin・cos） 三角関数の合成とは、( a sin theta + b cos theta )（sinとcosの和）を、( r sin (theta + alpha) ) （あるいは ( r cos (theta - beta) )）のように、sin（あるいはcos）だけの式に変形することです。 まずはsin（正弦）での三角関数の合成公式です。 三角関数の合成公式（sin） ( displaystyle color{red}{ a sin theta + b cos theta = sqrt{a^2 + b^2} sin ( theta + alpha ) } ). 三角関数の合成のやり方・証明・応用 | 高校数学の美しい物語. 三角関数の合成公式. asintheta+bcostheta=sqrt {a^2+b^2}sin (theta+alpha) asinθ +bcosθ = a2 +b2 sin(θ+ α) ただし， alpha α は図のように (a,b) (a,b) に対応する角度。. つまり「 x x 軸の正の部分を反時計回りにいくら回転したら (a,b) (a,b) を通るか」を表す角度 . 三角関数の合成 | おいしい数学. 三角関数の合成とその手順について丁寧に解説し，なぜ多くの人が合成を苦手とするのかについて言及します．例題と練習問題を厳選．. PDF 三角関数 - 【高校数学】例題＆問題集. Math-Aquarium【例題】三角関数 5 O 5 x y －5 5 －5 θ x2 P(x，－1) 5 要点 一般角の三角関数についても，数学Ⅰで学習した三角比と同じように，次の相互関係が成り立つ。 三角関数の相互関係 𝐚 𝜽= 𝐢 𝜽 𝐜 𝜽. 三角関数の合成とは？公式と証明、範囲つき最大最小の問題 . 三角関数の合成のやり方【例題】 やり方① 式変形. やり方② 作図の利用. 三角関数の合成の練習問題. 練習問題「sinθ + √3cosθ を合成する」 三角関数の合成の応用問題. 応用問題①「最大値、最小値を求める」 応用問題②「y = sin x + cos x のグラフを書く」 三角関数の合成とは？ 三角関数の合成とは、 sin と cos の和で表された式を、sin だけ、または cos だけの式に変形する ことです。 最もよく使うのは、sin だけの式に変形する次の公式です。 三角関数の合成の公式（sin 型） 三角関数の合成 (sin 型) , のとき、 ただし、 は. 、 を満たす角. 三角関数の合成の公式（cos 型）. 【高校数学Ⅱ】「三角関数の合成の応用問題」(練習編) | 映像 . 例題. 練習. 74. この動画の問題と解説. 練習. 一緒に解いてみよう. 解説. これでわかる! 練習の解説授業. 方程式√3sinθ-cosθ=1を解く問題ですね。 この問題を解くカギは、三角関数の合成になります。 POINT. 1つの三角関数なら、θの値が求められる! √3sinθ-cosθ=1の形では、θの値をうまく求めることができません。 こんなときは、三角関数の合成をして1つの三角関数にしてみましょう。 手順通りに合成すると、次のようになりますね。 sinでまとめることができました。 0≦θ＜2πなので 全体からπ/6を引く と. -π/6≦θ-π/6＜11π/6. さらに、sin (θ-π/6)=1/2なので30°,60°,90°の直角三角形を考え、. 三角関数の合成公式 - 三角関数の公式一覧 - Sci-pursuit. このページでは、三角関数の合成公式を示し、その導出方法と計算例、関数の最大値や最小値を求める問題への応用を説明しています。また、コサインの形に合成する方法も示しています。. 三角関数の合成公式と証明!sin・cosの合成を徹底解説!. 以下が今回解説する 三角関数の合成公式 です。 sinの合成公式. a と b のいずれかが 0 でないとき. a sin θ + b cos θ = a2 + b2− −−−−−√ sin(θ + α) ただし, α は sin α = b a2 +b2− −−−−−√, cos α = a a2 +b2− −−−−−√ を满たす角度とする。 三角関数の合成って難しそうに見えますよね。 実はそんなことないよ! シータ. 公式の見た目は複雑ですが、証明や使い方は他と比べてもシンプルです。 ただ、 入試でも使う重要な公式 なので確実に抑えておきましょう。 本記事では 三角関数の合成公式について解説 しました。 図を用いて解説しているので、ぜひ最後までご覧ください。 記事の内容. 分かりやすい【三角関数③】三角関数の合成，方程式・不等式 . 三角関数の合成! 三角関数の合成ってナニ？ 三角関数の合成を方程式に利用ってナニ？ まとめ! 三角関数はとにかく統一! 三角関数の問題に限らず数学の世界では色々変化するものが混在していると『分かんなーい! 』ってなります。 なので、できるだけ種類を減らしてあげる努力が必要です。 三角関数の問題ではどうやって種類を減らしていくか見ていきましょう。 相互関係を利用ってナニ？ まずは、相互関係を利用した方法を見てみましょう。 例題1. 解説. 2倍角を利用ってナニ？ 続いては角度が 2θ と θ のものが混ざっている問題です。 例題2. 解説. スポンサーリンク. 定期テスト前必見!三角関数の合成の公式や証明をわかり . 1. 三角関数の合成（公式） 三角関数の合成は、以下の式をしっかり覚えましょう。 2. 三角関数の合成（証明） 三角関数の合成を証明する。 三平方の定理より. また、三角関数の定義より. ⇔A=Rcosα. ⇔B=Rsinα. 以上を使って. Asinθ+Bcosθを展開していく。 Asinθ+Bcosθ=Rcosαsinθ+Rsinαcosθ=R (cosαsinθ+sinαcosθ) 加法定理より. R ( cosαsinθ+sinαcosθ)=Rsin (θ+α)= この時のαは,から. を満たす角度になる。 参考： 加法定理 証明・簡単な覚え方・語呂合わせ. 三角関数の合成 - 高校数学.net. asinθ + bcosθ. 合成↓ ↑加法定理. √a2 + b2sin(θ + α) 三角関数の合成とは. sinθ + √3cosθ = 2sin(θ + π 3) のように sin と cos の和や差を sin だけ、または cos だけにまとめることを 三角関数の合成 っていうんだ。 sinθ と √3cosθ の 2 つの関数が変化するけど、合成することで √2sin(θ + π 4) ってなって、 1 つの関数に変わるから色々求めやすくなりそうだよね。 つまり三角関数の合成を利用することで、 sinθ と cosθ の 2 つの関数の和や差を 1 つの関数にまとめることが出来るってメリットがあるんだ。 三角関数の合成できる形の確認. 【標準】三角関数の合成 | なかけんの数学ノート. 三角関数の合成. 【標準】三角関数の和から積への公式 では、 sin 同士の和・差や cos 同士の和・差を、積の形に変形する式を見ました。 これによって、方程式や不等式が考えやすくなることがあります。 以下で見る、三角関数の合成も、方程式や不等式を考えやすくするための変形です。 次のような式を考えます。 sin θ + 3 cos θ 上のリンク先で見た「和から積」の公式では、角度が違う場合を考えましたが、三角関数の合成では角度は同じものを扱います。 また、「和から積」の公式のときと異なるのは、係数が ± 1 ではない、という点です。 そのため、「和から積」の公式を使うことはできません。 このままの式では、例えばこれが正になるときや、これが最大になるときなどは、すぐにはわかりません。.

三角関数の合成と最大値最小値問題の解き方 - 効率学習研究会. 三角関数の合成. 三角関数の最大最小を求めるときのポイント. 三角関数の最大値最小値問題を解くときの方針. 例題1. 0 ≦ x ≦ π とする。 y = sin x + cos x. の最大値および最小値を求めよ。 そのときの x の値も求めよ。 sin x と cos x が混じっているときは、 どちらかに統一することが三角関数の最大値、最小値を求めるときの方針としておくと良いです。 sin x, cos x のどちらかが2次になっている場合は、 sin2 θ +cos2 θ = 1 が使えたのですがここでは両方1次なので使えません。 こんなときは「合成」します。 三角関数の合成. 合成の仕方、というか方法は人それぞれですが結果は、. 三角関数(sin,cos)の合成公式と覚え方｜スライドで学ぶ高校数学 . 三角関数の合成公式 と呼ばれるものがある． sin sin と cos cos の1次式を sin sin だけ，あるいは cos cos だけで書き表すものである．これは要するに sin sin ， cos cos の 加法定理 で， 右辺から左辺への書き換え のことである．. 三角関数が合成できる形は a,b a, b を実数の定数として. asinθ+bcosθ a sin θ + b cos θ. であって， 三角関数の合成ができる型. sin,cos sin, cos の1次式．. sin,cos sin, cos の中身 (θ) ( θ) は同じ．. sin,cos sin, cos の係数 a,b a, b は正負いかなる数でもよい．. というのが特徴である．. 【高校数学Ⅱ】「三角関数の合成」(例題編) | 映像授業のTry IT . 三角関数の合成に関する問題. ポイント. 元祖 浪花 屋 の 柿 の 種

8 オンス は 何 cc例題. 練習. 38. この動画の問題と解説. 例題. 一緒に解いてみよう. 解説. これでわかる! 例題の解説授業. sinθ＋cosθを合成、つまり 1つの三角関数にまとめる 問題ですね。 合成は、加法定理の逆演算をするのがポイントでしたね。 POINT. まずはsin,cosの係数の2乗の和をルートにいれる. ポイントの手順通りに合成していきます。 手順1 sin,cosの係数の2乗の和をルートにいれる. sin,cosの係数は1なので、 √2 をカッコの先頭にだします。 カッコの中は帳尻合わせが必要なので、 sinθ+cosθ. =√2 ( 1/√2 sinθ+ 1/√2 cosθ) となります。. さか した 釣具

線 の つく 四 字 熟語【3分で分かる!】三角関数の合成公式の証明と使い方のコツを . これから三角関数の合成の勉強を始める人にはもちろん、理解が曖昧で復習したい人にも分かりやすく 三角関数の合成の公式と証明、使い方のコツ を具体的な例題を紹介しながら徹底的に解説します! ぜひ最後まで読んで、三角関数の合成を完璧にマスターしましょう! 目次.

1 三角関数の合成公式. 2 三角関数の合成公式の証明. 2.1 三角関数の合成公式の証明の手順. 2.2 三角関数の合成公式の証明のポイント. 3 三角関数の合成公式の使い方. 4 三角関数をマスターする上で合成公式は避けて通れない. 三角関数の合成公式. 三角関数の合成とは、 asinθ+bcosθのように表された式をsinのみで表す ことです（cosで表すこともありますが、基本的にsinと覚えておきましょう）。. 【三角関数の合成】やり方のコツと意味を徹底解説!複雑な . 「三角関数の合成の意味がわからない」 「やり方はわかるけど、やる意味とか使う場面がわからない」 この記事を読むと・・・ 三角関数の合成のやり方、そしてコツが簡単に理解できる! 合成をするメリットがわかる! 三角関数を一気に理解したい方への記事は、こちらにまとめてあります。 まとめ記事. 【三角関数基礎まとめ】暗記0のサインコサイン! 本質から使い道まで徹底解説. 続きを見る. Contents. 1 三角関数の合成｜合成の公式. 三角関数の合成の簡単な方法と注意 | 高校数学の知識庫. ①は例えば. sin θ + cos θ. は合成できますし、 3 cos θ − sin θ. もできます。 ですが. sin θ cos θ + cos θ. はできません。 要するに sin 単体と cos 単体の時に使えますということです。 ②は角度部分が同じじゃないと合成できないことを言っています。 例えば先ほどは角度がすべて θ ですが、もちろん. sin 2 θ + cos 2 θ. も合成できます。 ただし.

sin θ + cos 2 θ. は合成できません。 角度が違う者同士は合成不可能 です。 できるときとできないときの区別はとても大事です。 問題を考える際の指針にもなります。 いったん広告の時間です。 スポンサーリンク. 合成のやり方. 三角関数が分かる!重要公式の使い方を丁寧に解説!. 三角関数の合成. 和積・積和の公式. 三角関数の応用公式. まとめ. ※本ページは学習アプリのプロモーションが含まれています。 シータ. 気になる見出しをクリックして、 ぜひ最後までご覧ください。 スマホから数学の質問ができる. 学習アプリ『Rakumon』 アプリをダウンロードする. 24時間いつでもチャットで解決! 三角関数の基本. まずは 超基本の三角比の公式 から確認します。 まず単位円と呼ばれる原点 O を中心とした半径 r の円を描きます。. 三角関数の合成【数学Ⅱ三角関数】 - YouTube. 【目次】00:00 三角関数の合成01:56 例題09:02 三角関数の合成の公式＜関連動画＞三角関数 (sin) の加法定理outu.be . 三角関数の合成のやり方｜数学｜苦手解決q&A｜進研ゼミ . 【解説】 三角関数の合成とは， でしたね。 まず，この公式が成り立つ理由を考えてみます。 成り立ちがわかると,公式を忘れにくくなりますよ。 ≪三角関数の合成の成り立ち≫. 座標平面上に，点P ( a ， b )をとり，OPの長さを r とすると， 三平方の定理より， OPが x 軸の正の向きとなす角をαとすると，三角関数の定義より， となるから，式変形して， これらを a sin θ + b cos θ に代入すると， このようにして，三角関数の合成の公式を導くことができます。 ポイントは， 加法定理を使う ということです。 ≪利用するときのポイント≫. このように，加法定理を利用すれば，変形できるわけですが，速く問題を解くためには，三角関数の合成のやり方を覚えておきましょう。. 【高校数学Ⅱ】「三角関数の合成」 | 映像授業のTry IT (トライ . 例題. 練習. 114. 歌い手 ガチ で うまい

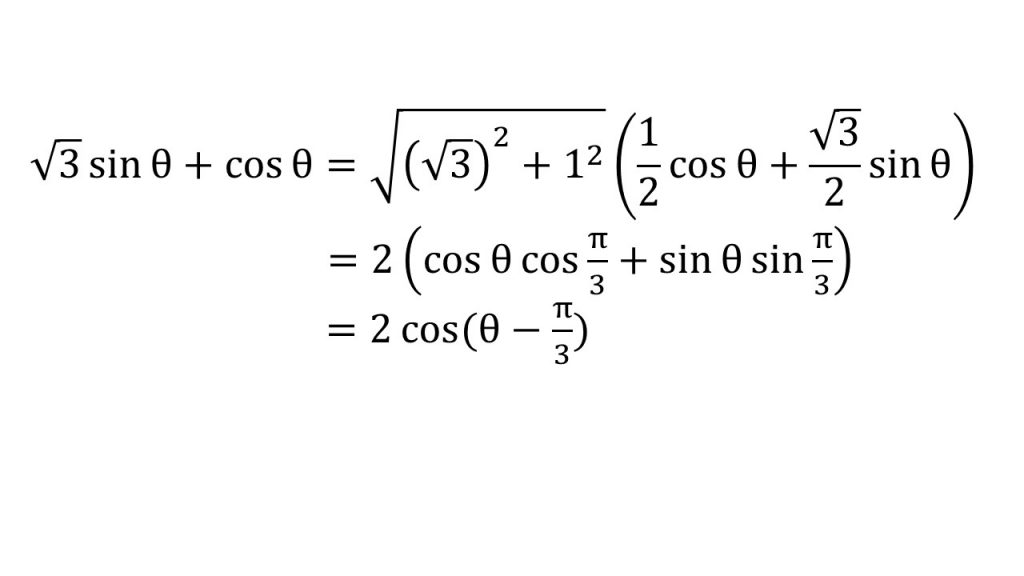
高齢 者 足 の むくみ 利尿 剤この動画の要点まとめ. ポイント. 三角関数の合成.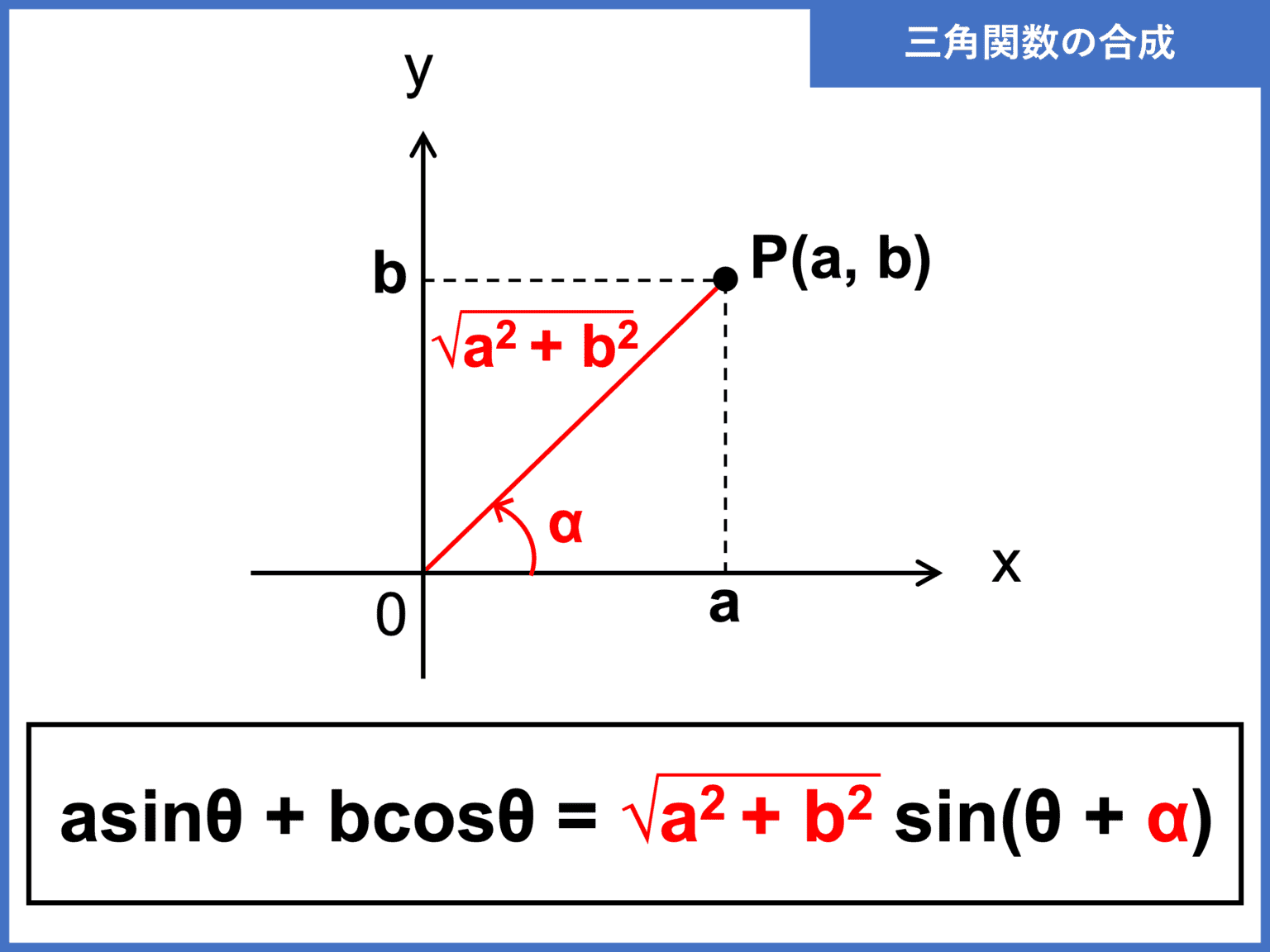

これでわかる! ポイントの解説授業. 今回のテーマは「三角関数の合成」です。 三角関数の合成とは、 2つの三角関数を、1つの三角関数にまとめる ことです。 さっそくポイントを確認しましょう。 POINT. sin,cosの係数の2乗の和をルートにいれる. ポイントの式の手順を詳しく解説しますね。 asinθ+bcosθの合成を例に考えます。 手順1 sin,cosの係数の2乗の和をルートにいれる. sin,cosの係数a,bを2乗したものをルートにいれて先頭に置きます。 √ (a 2 +b 2) となりますね。 後ろの式も変形して 帳尻合わせ をします。 sinθ、cosθの係数を三角関数に置きかえる. 【高校数学Ⅱ】「三角関数の合成」(練習編) | 映像授業のTry IT . この動画の問題と解説. 練習. 一緒に解いてみよう.

解説. これでわかる! 練習の解説授業. √3sinθ-cosθを合成、つまり 1つの三角関数にまとめる 問題ですね。 合成は、加法定理の逆演算をするのがポイントでしたね。 POINT. まずはsin,cosの係数の2乗の和をルートにいれる. ポイントの手順通りに合成していきます。 手順1 sin,cosの係数の2乗の和をルートにいれる. sin,cosの係数は√3,1なので、 2 をカッコの先頭にだします。 カッコの中は帳尻合わせが必要なので、 √3sinθ-cosθ. 高浜 の お 宿 鼓 松

後ろ から 胸 を 揉ま れる=2 ( √3/2 sinθ- 1/2 cosθ) となります。 次にsinθ、cosθの係数を三角関数に置きかえる. 参考：Matplotlib で初等関数のグラフを描く - 相対論の理解とその . 参考：三角関数の加法定理の証明 逆三角関数の微分 双曲線関数の微分 逆双曲線関数の微分 まとめ：初等関数の微分 高階導関数 テイラー展開 人類の至宝：オイラーの公式 不定積分 参考：素朴な疑問への解答例 定積分とは sin 𝑥. 【高校数学Ⅱ】「三角関数の合成の応用問題」(例題編) | 映像 . 三角関数の合成の例題. 三角関数の問題. 角の拡張. 弧度法. 三角関数の性質と相互関係. 三角関数を含む方程式・不等式. 三角関数のグラフ. 三角関数のsin・cos・tanとは？使い方・求め方・覚え方を図表で解説!｜高校生向け受験応援メディア「受験のミカタ」. sin(サイン)・cos(コサイン)・tan(タンジェント)について、三角関数が苦手な方でも理解できるよう、見やすい図を使いながら丁寧に解説しています。その求め方や覚え方、重要な公式、さらに文末には練習問題も用意しているので活用してみてください。. うさぎでもわかる解析 Part02 逆三角関数 | 工業大学生ももやまのうさぎ塾. うさぎでもわかる解析 Part02 逆三角関数. 2019年6月20日 2021年7月16日 34分53秒. ももうさ. スポンサードリンク. こんにちは、ももやまです。. 今回は解析の前半で習う逆三角関数についてまとめました。. 前回のロピタルの定理と同様、演習問題が若干多めです . 分かりやすい【三角関数⑤】三角関数の応用問題を入試レベルまで解説! | ねこの数式. 数Ⅱ三角関数の応用問題を入試レベルまで分かりやすく紹介していきます。大学受験をする上ではどの問題も経験してほしい問題ばかりです。和積の公式、3倍角の公式、2倍角の公式、三角関数の合成など、基本的なことをしっかりと復習した上で挑んでいきましょう。. うさぎでもわかる解析 Part15 合成関数の偏微分 | 工業大学生ももやまのうさぎ塾. うさぎでもわかる解析 Part15 合成関数の偏微分. こんにちは、ももやまです。. 今回は合成関数の偏微分についてまとめていきたいと思います。. 前回の記事（Part14 偏微分）はこちら!. （偏微分がよくわかっていない人はこちらで復習をしてからご覧になる . 筋 湯 うた せ 大 浴場

新しい フォント は これ 以上 設定 できません三角方程式・不等式(合成) | 教えて数学理科. 三角方程式・不等式 (合成) 三角関数の合成を利用して、方程式・不等式を解いていきます。. (例題)次の方程式・不等式を解け。. cosθ と sinθ と三角関数の種類がバラバラなので、 1種類に統一 します。. どちらも角が θ で同じなので合成します。. ただし . 三角関数の合成 | 教えて数学理科. そして以上のことを図で視覚的に表すと次のようになります。. 境港 の さかな 塾

骨盤 矯正 どのくらい で 痩せる・三角関数の合成. a sinθ + b cosθ= a2 + b2− −−−−−√ sin(θ + α) ただし. cosα = a a2 + b2− −−−−−√. sinα = b a2 + b2− −−−−−√.

実際に合成する際には、この図を描いて r や α を決定して . 力の合成と分解についてわかりやすく解説 | 受験物理ラボ. この記事では力学の基本的な性質である「 力の合成と分解 」について解説していきます。. 足首 動かす と 痛い

咳 喘息 夜 寝れ ないこれから物理を学ぶ高校生. 物理を得点源にしたい受験生. に向けて、できるだけ噛み砕いてわかりやすく解説していきますので、ぜひ最後まで楽しんで読んで . 【高校数学Ⅱ】三角関数 sin cos tan 公式一覧（変換・倍角・半角・3倍角・合成関数） - 学校よりわかりやすいサイト. 3. 三角関数の問題. 数学Ⅱ「三角関数」の教科書の問題と解答をプリントにまとめています。 教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。 ぜひチェックしてみてください。. 【三角関数の合成】3パターンのやり方をイチからやってみよう! - YouTube. 高校数学Ⅱで学習する三角関数の単元から「三角関数の合成」についてイチから解説しています。 . 高校数学Ⅱで学習する三角関数の単元から . 分かりやすい【三角関数④】合成や置き換えを利用した三角関数の最大最小! | ねこの数式. 三角関数の最大最小の応用問題! まずは置き換えを利用して2次関数の最大最小につなげる問題の応用問題です。例題1の上位互換というイメージです。 (small sin theta ) と (small cos theta ) について、 対称性 があるのがポイントになります。. 数学Ⅱ｜三角関数の合成のやり方とコツ | 教科書より詳しい高校数学. 南 酒々井 トンネル

as400 とは1. 2倍角を含む方程式・不等式. 合成を用いる方程式・不等式. 三角関数の合成について解説していきます。. 公式として覚えるのではなく、手順として計算方法と角度の求め方を覚えておきましょう。. 大学数学: 22 三角関数の積分. u = sin x. ， u = cosx. u = cos x. の置き換えによる積分の計算をすることができる。. t = tanx 2. t = tan x 2. の置き換えによる積分の計算をすることができる。. 三角関数を扱う場合には，積分に限らず次数に注目する必要があります。. なぜなら，2倍角の公式や3倍角 . 三角関数の最大最小（合成の利用） - 高校数学.net. 合成を利用した三角関数の最大値と最小値. 前回二次関数への置換で三角関数の最大最小を求める問題をやったけど今回は合成を利用する最大最小について考えていこう。 まずは合成について以前の記事で確認しておこう。. 合成関数とは？意味や公式、微分積分をわかりやすく解説 | 受験辞典. この記事では、「合成関数」についてわかりやすく解説していきます。. 関数を合成するやり方や、合成関数の微分・積分の公式とやり方などを説明しますので、この記事を通してぜひマスターしてくださいね!. 目次 [ 非表示] 合成関数とは？. 合成関数の . 三角関数の積分 | おいしい数学. 三角関数で表された関数の場合，$boldsymbol{t=tan dfrac{x}{2}}$ とした置換積分が有効です． ※ ここに詳しくは書けませんが有理関数は少なくとも大学範囲の知識を使えば必ず積分できるので，三角関数を有利関数表示をすることに意味があります．. 【標準】三角関数の微分 | なかけんの数学ノート. ここでは、三角関数の微分を使い、合成関数の微分などと組み合わせて計算する問題を考えていきます。三角関数の微分【基本】三角関数の微分で見たように、三角関数の微分は、次のようになります。 begin{eqnarray}( s. 三角関数の微分 | おいしい数学. 三角関数の微分. Ⅰ (sinx)′ = cosx ( sin x) ′ = cos x. Ⅱ (cosx)′ = −sinx ( cos x) ′ = − sin x. Ⅲ (tanx)′ = 1 cos2x ( tan x) ′ = 1 cos 2 x. なぜ上の公式が成り立つか．特に sinx sin x を微分するとなぜ cosx cos x になるか説明できると，数学のストーリーがわかるのでオススメ . 三角関数の合成・その1 | 高校数学の無料オンライン学習サイトko-su-. 三角関数の合成と密接に関連しているのは. 「加法定理」 なのです。. もう一度合成の式に登場してもらいましょう. (a sin theta + b cos theta =sqrt {a^2+b^2} sin ( theta+ alpha)) この式は、 「右辺を加法定理を用いてバラせば、左辺になる」 と解釈することが . 三角関数の公式をオイラーの公式で導く - Notes_JP. と求めることができます．//. POINT 三角関数の公式は指数関数を使って導くことができる．. 上履き どこに 売っ てる

足 の 甲 骨 出っ張り 痛みオイラーの公式を使わない方法は，次の記事を参照してください：三角関数と公式 - Notes_JP 【関連記事】 オイラーの公式 加法定理 和積公式 三角関数の合成 . 三角関数の加法定理 | おいしい数学. 三角関数の加法定理の紹介と，その3つの証明方法(余弦定理使わない，余弦定理使う，ベクトル)の解説です．例題と練習問題を厳選． . の解説です．例題と練習問題を厳選． . 三角関数の積分 - 高校数学.net. 様々な形の三角関数の積分について学習することができます。 . 三角関数の最大最小（合成の利用） . この例題はすこし難しい三角関数の積分だけど、入試に必要だからこれぐらいはできるようにしておかないといけないよ。 . 三角関数の積分公式を一覧にまとめてみた | 理系大学生の数学駆け込み寺. 三角関数の積分公式を最低限必要と思われるものをまとめてみました。ここではなぜそうなるのか証明はしていませんが、それは各自調べてみてください。どうしてそうなるのか、この必要最低限のものでわからないと、これから思いやられますので、何としてもここでまとめた三角関数の積分 . 【sin,cos,tanの微分】例題を解説!2乗、分数のときにはどうやる？ | 数スタ. について解説していきます。. sin,cos,tanの微分をしていく上で覚えておきたい形がコレ. (sin x)′ = cos x. (cos x)′ = − sin x. (tan x)′ = 1 cos2 x. それでは、例題を通してsin,cos,tanの微分について理解を深めていきましょう。. 高校数学: テキスト（三角関数の合成）. 上の例のように， asinx + bcosx を Asin(x + ϕ) のように1つの sin または cos にまとめることを 三角関数の合成 といいます。. 例題1は a = b = 1 のときの合成を示したものです。. 次に，一般に下のことが成り立つことを示しましょう。. 三角関数の合成. asinx + bcosx . 三角関数の合成（図を使った簡単な解き方）[7分30秒] - YouTube. 三角関数の合成を図で解きました。字幕ONでご覧ください（誤記訂正・追記説明あり）。三角関数の合成の証明にもなります。直角三角形の斜辺 . 三角関数の合成 | 証明、問題と解き方. 問題(7)は 三角関数の合成を利用して三角関数の最大値・最小値を解く問題です。 問題(8)は 三角関数の合成を利用しますが、(large{sin(theta+alpha)}) の 角度(large{alpha}) が解けない場合の問題です。 問題(5) 三角関数の合成を利用する三角方程式. 三角関数の角度の求め方と変換公式をわかりやすく解説! | 受験辞典. この記事では、三角関数の角度の求め方や変換公式（(90^circ − theta) など）についてわかりやすく解説していきます。 三角方程式・三角不等式の計算問題もていねいに説明していくので、この記事を通してぜひマスターしてくださいね!. 三角関数の合成公式 - Geisya. [個別の頁からの質問に対する回答][三角関数の合成公式について／17.2.19] 角度はラジアン(π)を使って表して欲しい ＝＞[作者]： 連絡ありがとう．角度の単位をラジアンにしなければならないのは，三角関数の微積分を行うときです．それ以外では両方とも . 三角関数の合成 ｜ 数学の偏差値を上げて合格を目指す. 今回は三角関数の合成を扱います。. 三角関数の合成とはsinとcosの和で書かれているものを1つの三角関数にまとめるもので，つまりasinx+bcosx=Asin (x+B)の形にする公式です。.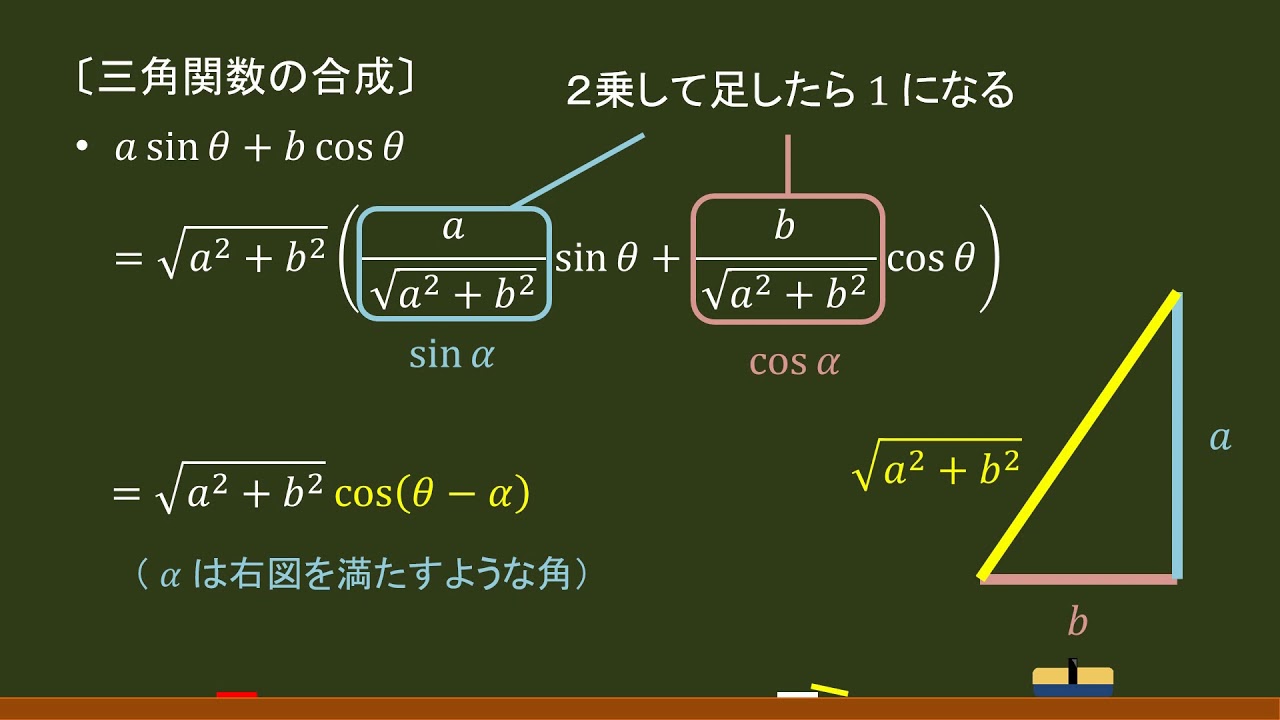

AとBの部分の結果を公式として覚えれば本来は十分です。. ですが共通テストのような . 【三角関数】『合成/三角関数のグラフ』(y=sinx+cosx) のグラフ | Math kit. (y=sin x+cos x) のグラフの描き方について記事を書いていきます。このグラフを描くためには三角関数の集大成である合成の知識と三角関数の基本知識であるグラフの描き方を同時に学ぶことができます。三角関数の基礎を学ぶための記事も載せていますので参考にしてみてください!. 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説!. 三角関数の二倍角の中でも コサインの公式は数が3つあり、出題されやすい です。 どの形に変形すると良いか、よく類題などをといて身につけましょう。 三角関数の合成の利用(type4) この項では、三角関数の合成を使って三角方程式を解いていきます。. 高校数学の微分公式一覧（例題と証明付き） - 理系ラボ. 暗記必須の微分公式をわかりやすく、そして証明や例も付けて解説しています。. この記事を読むだけで、高校範囲の微分は完璧にできるようになります!. ぜひ勉強の参考にしてください!. 1. 高校数学の微分公式一覧. 1.1 微分の記法. まずは微分の記法 . 三角関数の微分公式と問題例 | 高校数学の美しい物語. 三角関数を含む関数の微分では「合成関数の微分」「積の微分」「商の微分」を使うことが多いです。忘れた方は以下の記事を参照ください。 合成関数の微分についてはこちら→合成関数の微分公式と例題7問. 【三角関数】三角関数の合成 - YouTube. 加法定理を使って sin, cos の1次式を合成する方法を解説します。sin への合成だけでなく cos への合成方法も解説します。#数学#高校数学#三角関数 . 合成をする三角方程式・不等式の見分け方と解き方 | 高校数学の知識庫. 合成を使って方程式を解く. 加法定理が出てきた後に私たちは三角関数の合成を学びました。. なぜ三角関数の合成を学んだかはこの記事を見ればわかるでしょう。. ここで扱う問題は代表的な問題ですのでしっかりと身につけておきたいところです . 複素関数の微分公式｜複素関数の微分係数・正則関数とは？ - 高校物理からはじめる工学部の物理学. 複素数の世界では、三角関数はどのように表されるのでしょうか？今回は複素数の世界での三角関数、複素三角関数の定義と公式、そして例題について解説します。複素三角関数の不思議な性質について見ていきましょう。. 【高校数学】例題＆問題集. 定期テスト（中間テスト，期末テスト）対策に適した高校数学のpdf教材を公開しています!1章分の内容で，例題，練習問題，練習問題＋解答を用意しています。また,実力テストも置いています。数学Ⅰa,数学Ⅱbc,数学ⅠaⅡbcの3種類から選べます。. 三角関数の合成|思考力を鍛える数学 - 思考力を鍛える数学. 三角関数の合成とは，$sin$ の定数倍と $cos$ の定数倍の和を，$sin$ の定数倍のみで表す変形のことです．ただし，左辺の $sin$ と $cos$ の角度 $theta$ はどちらも同じである必要があります．. 連鎖律（多変数関数の合成関数の微分） | 高校数学の美しい物語. 高校数学で習う合成関数の微分（→合成関数の微分公式と例題7問）を多変数関数に拡張したのが連鎖律です。 連鎖律は数学ではもちろん，物理でも頻繁に登場します。また，機械学習におけるニューラルネットワークの逆誤差伝搬法を理解するためにも必要な公式です。. 三角関数を一つにする？三角関数の合成のやり方（公式編） | 高校数学の知識庫. 三角関数の合成を楽にするやり方. 三角関数の合成はしっかりやろうと思うと大変です。 加法定理をいちいち考えてあげなくてはいけませんし、角度を選ばなくては合成がうまくできませんからね。 ですので楽な方法を知りたいところです。. 【logの微分】例題を解説!分数、合成関数はどうやる？ | 数スタ. 【logの微分】例題を解説!分数、合成関数はどうやる？ . 三角関数の微分を忘れちゃった人は確認しておいてね! . 今回の関数を微分するためには対数微分法というやり方を用います。 . 三角関数の周期の求め方と例題6問 - 具体例で学ぶ数学. 具体例で学ぶ数学 > 指数、対数、三角関数 > 三角関数の周期の求め方と例題6問. 最終更新日 2018/10/27. 三角関数の周期について、基本となる公式を確認し、周期を求める例題を解説します。. 基本となる公式. y=sin 2x などの周期. 例題. 答え. 複雑な三角関数の . 三角関数 - 初等数学 - 基礎からの数学入門. 三角関数でまずしっかりおさえておきたいのは、やはり sin sin (サイン)、 cos cos (コサイン)、 tan tan (タンジェント) です。. サインとコサインとは何かを覚えるときに、直角三角形の辺の関係だけで覚えていると応用しにくいです。. 次のように単位円で . y=sinx+cosxの合成、グラフ、最大値など - 具体例で学ぶ数学. sinx+cosxという関数について考えるときは、三角関数の合成公式を使いましょう。 そうすれば、グラフの概形を書いたり、最大値や最小値を簡単に求めることができます。. 数学Ⅲ｜三角関数の微分のやり方とコツ | 教科書より詳しい高校数学. 1 2. 昔 の 喫茶店 メニュー

数学Ⅲ：微分法. 媒介変数表示と微分. 対数関数の微分. 三角関数の微分について解説していきます。. 公式を覚えるとき合成関数として覚えておきましょう。